Rangkuman Materi Fisika Besaran dan Pengukuran

Untuk adik-adik siswa SMP, berikut ini kami akan membagikan Rangkuman Materi Fisika Besaran dan Pengukuran. Semoga rangkuman materi ini bermanfaat.

A. Besaran dan Satuan

Besaran adalah sesuatu yang dapat diukur dan dapat dinyatakan dengan bilangan dan satuan.

Satuan adalah sesuatu yang menyatakan ukuran suatu besaran yang diikuti bilangan.

Besaran dalam fisika terbagi menjadi dua:

a. Besaran pokok, yaitu besaran yang satuannya telah ditentukan secara internasional (SI) sebagai dasar besaran lain (turunan). Tujuh besaran pokok:

b. Besaran turunan, yaitu besaran yang satuannya diturunkan dari besaran pokok. Beberapa besaran turunan, yaitu:

Besaran berdasarkan arahnya terdiri dari:

a. Besaran skalar, besaran yang tak punya arah. Contoh: massa (m), panjang (L), waktu (t), kelajuan (v), massa jenis (ρ).

b. Besaran vektor, besaran yang punya arah. Contoh: gaya (F), percepatan (a), kecepatan (v), momentum (p).

B. Dimensi Besaran

Dimensi besaran adalah cara suatu besaran tersusun atas besaran pokok.

Contoh:
Tentukan dimensi besaran gaya dan usaha!
Gaya:
F = m.a
F = M.L/T²
F = M.L.T^–²
Usaha:
W = F.s
W = M.L.T^–².L
W = M.L².T^–²

Dimensi besaran dapat digunakan untuk:

a. Membuktikan kesetaraan dua besaran
Contoh:
Buktikan bahwa besaran momentum dan impuls adalah besaran yang setara!
Momentum
P = m.v
P = M.L.T^-1
Impuls
I = M.L.T^-2 .T = M.L.T^-1
kedua besaran tersebut setara.

b. Membuktikan kebenaran suatu persamaan atau rumus
Contoh:
Buktikan bahwa rumus λ = v.t bernilai benar!
λ = v.t
L = L.T^-1.T
L = L
berarti rumus tersebut benar.

C. Pengukuran

Pengukuran adalah membandingkan suatu besaran yang diukur dengan besaran lain.

Beberapa perbandingan internasional pada besaran pokok per satuannya:

1) Panjang
Satu meter didefinisikan sebagai jarak yang ditempuh cahaya dalam vakum, dalam selang waktu 1/299.792.458 s.

2) Massa
Satu kilogram didefinisikan sebagai massa 1 liter air murni bersuhu 4°C.

3) Waktu
Satu detik didefinisikan sebagai waktu yang diperlukan atom cesium-133 untuk bergetar sebanyak 9.192.631.770 kali.

4) Kuat arus listrik
Satu Ampere didefinisikan sebagai kuat arus yang dialirkan melalui dua buah kawat yang sejajar dan diletakkan pada jarak pisah 1 m dalam vakum, menghasilkan gaya 2 x 10^-7 N tiap meter kawat.

5) Suhu
Satu Kelvin didefinisikan sebagai 1/273.16 kali suhu termodinamika titik tripel air.

6) Intensitas cahaya
Satu candela didefinisikan sebagai intensitas cahaya suatu sumber cahaya yang memancarkan radiasi monokromatik pada frekuensi 540 x 10¹² Hz dengan intensitas radiasi sebesar 1/683 W/Sr.

7) Jumlah zat
Satu mol didefinisikan sebagai jumlah zat yang mengandung zat elementer sebanyak atom yang terdapat pada 0.012 kg karbon-12.

Walaupun telah memiliki definisi, pengukuran masih memiliki kesalahan atau ketidakpastian dalam pengukurannya.

Kesalahan pengukuran sistematis diakibatkan:
a. Keterbatasan ketelitian alat ukur.
b. Kesalahan pengaturan/kalibrasi alat ukur.
c. Kesalahan sudut pandang (paralaks) saat membaca alat ukur.
d. Kesalahan akibat penyederhanaan nilai/sistem.
e. Pengukuran tunggal sehingga tidak akurat.

Oleh karena itu, kesalahan relatif atau batas suatu toleransi pengukuran harus selalu dicantumkan dalam hasil pengukuran.

Pengukuran tunggal adalah pengukuran yang dilakukan terhadap suatu besaran sebanyak satu kali saja.

Nilai kesalahan pengukuran tunggal antara lain:

a. Kesalahan mutlak
Δx = 1/2 x ketelitian

b. Kesalahan relatif
KR = Δx/x
dengan persentase kesalahan relatif
%KR = Δx/x x 100%

Pengukuran berulang adalah pengukuran yang dilakukan terhadap suatu besaran secara berulang untuk mendapatkan akurasi.

Nilai kesalahan pengukuran berulang antara lain:

a. Kesalahan mutlak
Δx = (Σ|x_i-x̅|)/n

b. Kesalahan relatif
KR = Δx/x
dengan persentase kesalahan relatif
%KR = Δx/x x 100%

Keterangan:
x_i = data pengukuran i
x̅ = rata-rata hasil pengukuran
n = jumlah percobaan

Penulisan akhir hasil pengukuran:
l = x ± Δx
l = x ± KR

D. Pengukuran Panjang

Dalam pengukuran panjang, dapat digunakan:

a. Penggaris/mistar
Penggaris adalah alat ukur panjang dengan ketelitian 1 mm/0,1 cm.

Pengukuran
x = x2 – x1
x = 7,2 – 0,5
x = 6,7
∆x = 1/2 x ketelitian
∆x = 1/2 x 0,2 cm
∆x = 0,05 cm
l = x ± Δx
l = 6,7 ± 0,05 cm

b. Jangka sorong
Jangka sorong adalah alat ukur panjang dengan ketelitian 0,1 mm/0,01 cm.

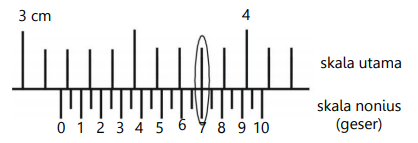
Panjang pada skala utama (x_utama) adalah skala yang terdapat di sebelah kiri titik 0 skala nonius.
Panjang pada skala nonius (x_nonius) adalah skala yang berimpit dengan skala utama.

Pengukuran
x utama = 3,1 cm
x nonius = 0,07 cm
x = x_utama + x_nonius
x = 3,1 + 0,07
x = 3,17 cm
Δx = 1/2 x ketelitian
Δx = 1/2 x 0,01 cm
Δx = 0,005
l = x ± Δx
l = 3,17 ± 0,005 cm

c. Mikrometer sekrup
Mikrometer sekrup adalah alat ukur panjang dengan ketelitian 0,01 mm/0,001 cm.

Panjang pada skala utama (x_utama) adalah skala terpanjang yang masih dapat terbaca.
Panjang pada skala nonius (x_nonius) adalah skala yang berimpit dengan skala utama.

Pengukuran:
x_utama = 3,5 mm
x_nonius = 0,37 mm
x = x_utama + x_nonius
x = 3,5 + 0,37
x = 3,87 mm
Δx = 1/2 x ketelitian
Δx = 1/2 x 0,01 mm
Δx = 0,005 mm
l = x ± Δx
l = 3,87 ± 0,005 mm

E. Pengukuran Massa

Dalam pengukuran massa, dapat digunakan:

a. Neraca lengan/Ohaus

Neraca lengan adalah alat ukur massa dengan ketelitian 0,01 g.

Neraca lengan terdiri dari tempat beban, skala beban, beban geser, sistem pengatur khusus dan penunjuk.

Cara pengukuran massa menggunakan neraca lengan:

1. Atur beban geser pada posisi nol dan sistem pengatur khusus, sehingga neraca lengan berada dalam keadaan seimbang.
2. Letakkan benda yang akan diukur pada tempat beban.
3. Atur beban geser yang ada sehingga neraca seimbang.
4. Jumlahkan seluruh bacaan skala masingmasing lengan skala yang merupakan massa benda yang diukur.

b. Neraca pegas

Neraca pegas adalah alat ukur massa dengan ketelitian 0,5 g.

Neraca pegas terdiri dari pegas dan selongsong besi yang ujungnya terdapat pengait.

Cara pengukuran massa dengan neraca pegas adalah dengan menggantung benda yang akan diukur pada pengait neraca. Bacaan skala yang ditunjuk oleh penunjuk neraca sama dangan massa benda yang diukur.

F. Pengukuran Waktu

Dalam pengukuran waktu, biasanya digunakan stopwatch.

Stopwatch analog adalah alat ukur waktu yang memiliki ketelitian 1 s, adapun stopwatch digital dapat memiliki ketelitian yang lebih presisi.

Stopwatch analog terdiri dari tombol dan jarum penunjuk.
a. Tombol stopwatch terdiri dari tombol mulai, berhenti dan reset. Tombol reset berfungsi untuk mengembalikan jarum penunjuk ke posisi nol.
b. Jarum jam terdiri dari jarum besar dan jarum kecil. Jarum besar adalah jarum yang menunjukkan menit, sedangkan jarum kecil adalah jarum yang menunjukkan detik.

Cara pengukuran waktu menggunakan stopwatch:

1. Tekan tombol reset lalu lepaskan sehingga jarum penunjuk kembali ke posisi nol.
2. Tekan tombol mulai lalu lepaskan ketika hendak memulai pengukuran.
3. Tekan tombol berhenti lalu lepaskan ketika pengukuran tepat selesai.
4. Hasil akhir adalah penjumlahan bacaan jarum besar (menit) dengan bacaan jarum kecil (detik).

G. Angka Penting

Angka penting adalah angka yang dihasilkan dari hasil pengukuran (bukan penghitungan), termasuk angka yang ditaksirkan.

Contoh: Pada hasil pengukuran 8,9 cm, Angka 8 merupakan angka pasti, dan 9 merupakan angka taksiran.

Aturan dalam penggunaan angka penting:

a. Semua angka selain nol adalah angka penting (a.p.).
Contoh:
3,21 (3 a.p.)
2,2 (2 a.p.)
1,559 (4 a.p.)

b. Angka nol yang terletak di antara dua angka adalah angka penting.
Contoh:
3,01 (3 a.p.)
2,5009 (5 a.p.)
20,09 (4 a.p.)

c. Angka nol yang terletak di belakang koma desimal adalah angka penting.
Contoh:
3,00 (3 a.p.)
9,0 (2 a.p.)
44,500 (5 a.p.)

d. Seluruh angka nol yang terletak di sebelah kiri koma desimal dan menyatakan bilangan <1 bukan angka penting.
Contoh:
0,1 (1 a.p.)
0,0088 (2 a.p.)
0,00609 (3 a.p.)

e. Semua angka nol yang terletak di kanan angka bukan nol namun tidak diikuti koma desimal bukan angka penting, kecuali diberi tanda.
Contoh:
1205000 (4 a.p.)
22400 (3 a.p.)
1205000 (6 a.p.)
22400 (4 a.p)

Aturan pembulatan bilangan dalam fisika adalah sebagai berikut:

a. Angka yang nilainya >5 dibulatkan ke atas.
Contoh:
6,38 dibulatkan menjadi 6,4

b. Angka yang nilainya <5 dibulatkan ke bawah.
Contoh:
8,34 dibulatkan menjadi 8,3

c. Angka yang nilainya =5 dibulatkan ke atas jika angka sebelumnya ganjil, dan dibulatkan ke bawah jika angka sebelumnya genap.
Contoh:
4,25 dibulatkan menjadi 4,2
5,55 dibulatkan menjadi 5,6

Operasi hitung angka penting harus mengikuti aturan berikut:

1) Penjumlahan dan pengurangan
Hasil dari operasi menghasilkan hanya satu angka taksiran saja dan angka penting paling sedikit.
Contoh:
23,12 + 1,2 = 24,32 dibulatkan 24,3 (3 a.p.)
21,9 – 1,15 = 20,75 dibulatkan 20,8 (3 a.p.)

2) Perkalian dan pembagian
Hasil dari operasi menghasilkan banyak angka penting yang paling sedikit dari bilangan yang dioperasikan.
Contoh
Contoh:
12,2 (3 a.p.) x 3,5 (2 a.p.) = 42,70 dibulatkan 43 (2 a.p.)
3214 (4 a.p.) x 121 (3 a.p.) = 388894 menjadi 388000 (3 a.p.)
1,44 (3 a.p.) : 7,2 (2 a.p.) = 0,2 menjadi 0,20 (2 a.p.)
2564 (4 a.p.) : 12 (2 a.p.) = 213,666… menjadi 210 (2 a.p.)

3) Pemangkatan dan penarikan akar
Hasil dari operasi menghasilkan banyak angka penting yang sama dengan bilangan yang dioperasikan.
Contoh:
(2,5)2 = 6,25 ≈ 6,3 (2 a.p.)
√225 = 15 ≈ 15,0 (3 a.p.)

4) Perkalian dan pembagian dengan bilangan eksak
Hasil dari operasi menghasilkan banyak angka penting yang sama dengan bilangan hasil pengukuran.
Contoh:
Suatu benda panjangnya 1,25 m jika diperpanjang menjadi 4 kalinya, maka,
1,25 x 4 = 5,00 (3 a.p.)

Notasi ilmiah adalah notasi yang menyederhanakan bilangan yang sangat kecil atau sangat besar menjadi satu tempat satuan.
a x 10ⁿ
a = bilangan pokok/mantisa (1 < a < 10)
10ⁿ = orde besar
n = orde bilangan
Contoh:
0,0000000257 menjadi 2,57 x 10^-8
965300 menjadi 9,653 x 10⁵